Переменный электрический ток

Переменным называют такой ток, величина которого меняется во времени.

По форме переменные токи подразделяются на периодические и непериодические.

Постоянный ток

Переменный непериодический ток

Переменный периодический ток (импульсы)

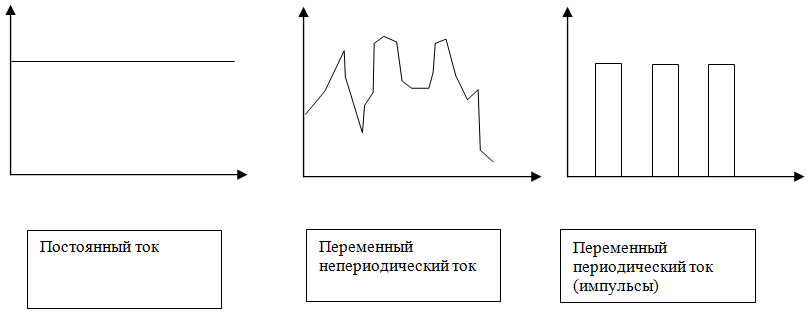
Периодические токи бывают несинусоидальные и синусоидальные.

Токи могут быть изменяющиеся по направлению и не изменяющиеся по направлению.

Наибольшее значение в электротехнике имеют синусоидальные токи. Синусоидальные токи производятся генераторами переменного тока.

Зачем нам переменный ток?

Этого не понимал даже великий Эдиссон. Он считал, что логичнее и проще использовать постоянный ток. Вся современная электроэнергетика – это энергетика переменного тока.

Дело в том, что переменное напряжение легко менять - повышать и понижать. Это очень важно! Например, для передачи электроэнергии на расстояние. Переменное напряжение можно поднять трансформатором до сотен тысяч Вольт и с минимальными потерями передавать электроэнергию на тысячи км.

Распределять электроэнергию в местных сетях тоже выгоднее в виде переменного тока.

Переменный ток легче производить – генераторы переменного тока проще и дешевле, чем генераторы постоянного тока.

Переменным током можно крутить самые надежные и недорогие электродвигатели - асинхронные, на них построена вся промышленность.

В быту и промышленности – везде используется переменный ток.

В домашних розетках действует переменное напряжение 220 Вольт. На это напряжение рассчитаны лампочки освещения, утюги, стиральные машины, пылесосы, электроинструмент и все остальные бытовые приборы. Электронные устройства – радио и теле аппаратура питаются постоянным током, но включаются они вилками в розетки 220 Вольт, а преобразование делается уже в самих аппаратах.

В промышленных помещениях используется переменное напряжение 220 Вольт и 380 Вольт. Под 380 Вольт подключают промышленное оборудование.

Нужно научиться считать токи, напряжения и мощности в цепях переменного тока, Это необходимо для правильного выбора источников, переменного напряжения и правильного выбора потребителей переменного тока.

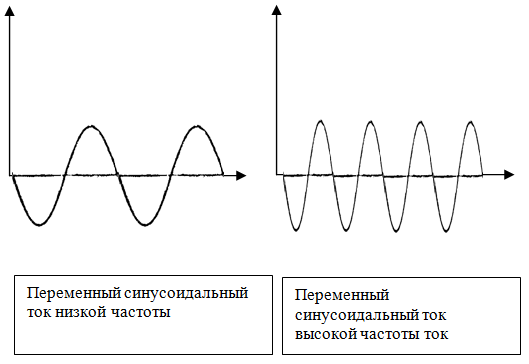
В основе рассуждений о переменных процессах в электрических цепях лежат свойства синусоидального переменного процесса, то есть, гармонических колебаний.

Гармонические колебания

Гармоническое колебание изображается синусоидой

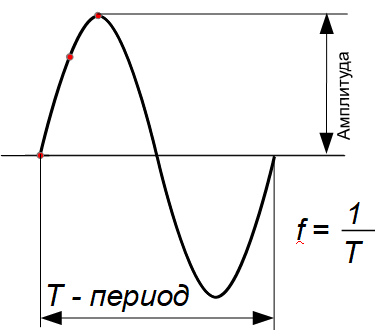
График изображает изменение значения переменной величины. В каждый следующий момент времени величина становится другой и если изменение происходит по закону синуса, то получается синусоида. Синусоида это изображение гармонического колебания.

Основные параметры синусоиды - Период  Т в секундах, частота f  в Гц и Амплитуда

Гармония – это согласованность, слаженность, взаимная обусловленность частей в целом. Синусоидальное колебание происходит равномерно без рывков и неожиданных изменений, оно полностью предсказуемо. Синусоида получается как линейная развертка равномерного вращения.

Колебание напряжения от источника получается гармоническим - синусоидальным, потому, что процесс генерации этого напряжения происходит симметричной круглой конструкцией с равномерно вращающимся ротором.

Генератор переменного тока   

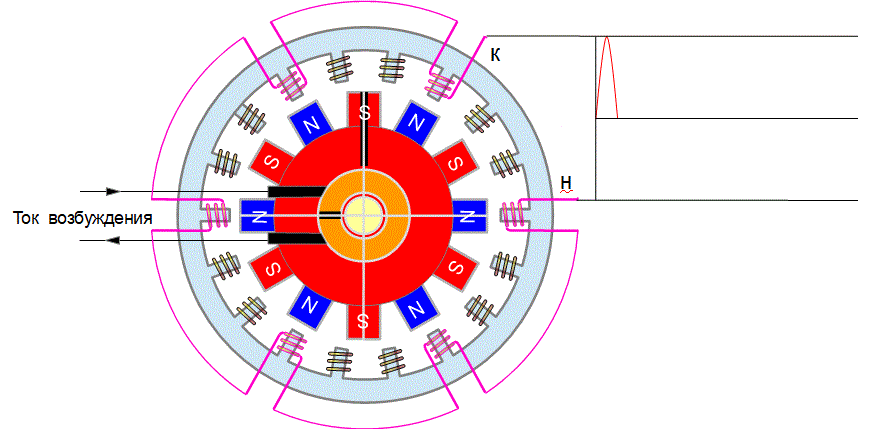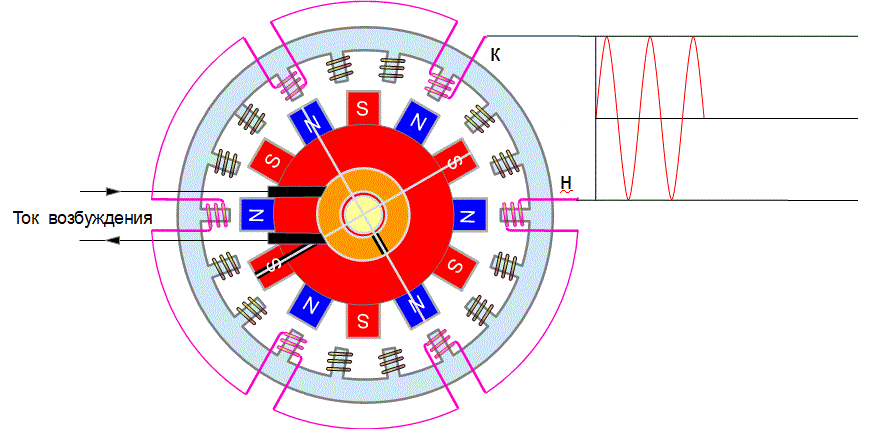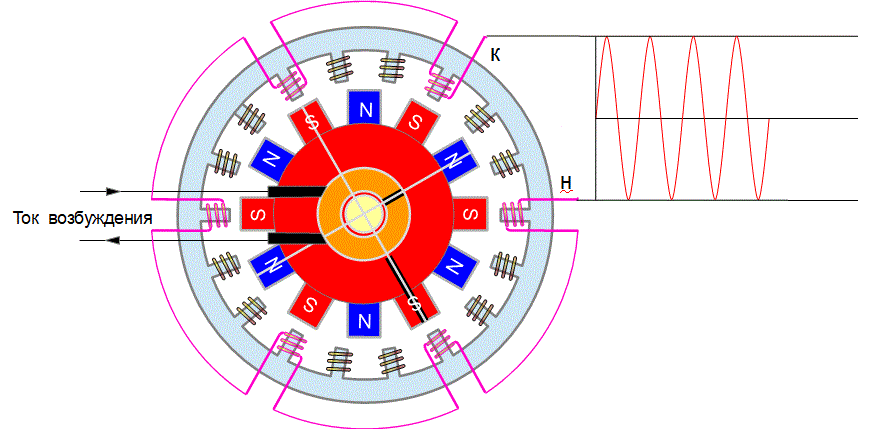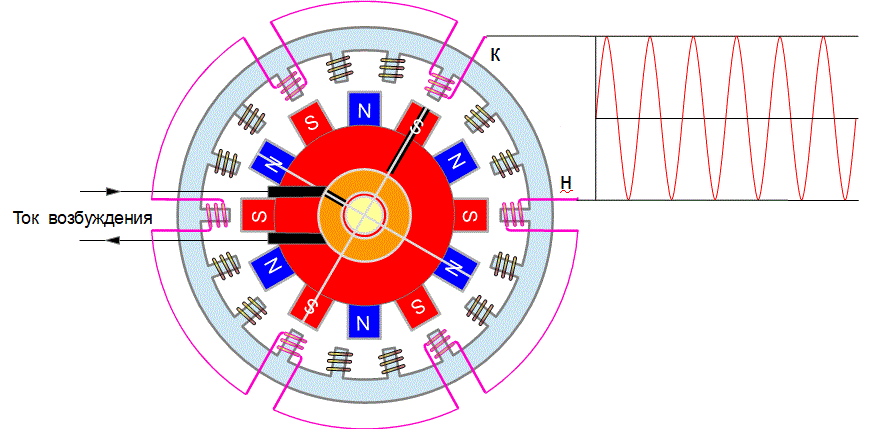
Переменное напряжение, которое получается на выходе обмотки этого генератора, получается примерно синусоидальным.

На самом деле получить идеально синусоидальный процесс невозможно, но мы будем рассматривать именно гармонический процесс как наиболее простой, а всеми отклонениями от синусоидального процесса для начала можно пренебречь.

Синусоида достаточно сложная кривая и расчеты всех значений по синусоиде затруднительны. Более просто те же самые процессы гармонического колебания можно изобразить вращающимся вектором. Синусоида строится как набор точек, которые соответствуют положению конца радиус – вектора. Радиус – вектор переменной величины равен ее максимальному значению, а изменения переменной величины отражаются положением этого вектора.

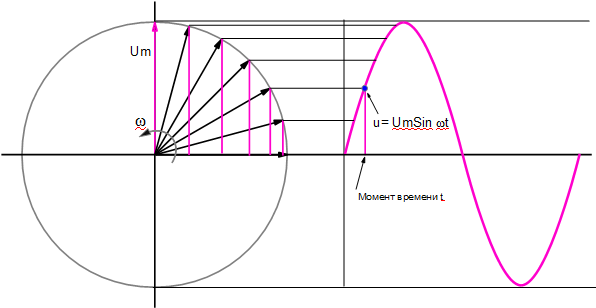
Мгновенное значение переменной величины (точка на синусоиде) соответствует данному положению вращающегося радиус – вектора. Вертикальная проекция радиус вектора, определяет мгновенное значение переменной величины. Эта проекция радиус-вектора - противолежащий катет треугольника, а он, как известно, равен радиус вектору (гипотенузе) на синус угла поворота радиус вектора. То есть, положение точки – ее высота на синусоиде определяется синусом угла поворота радиус-вектора.

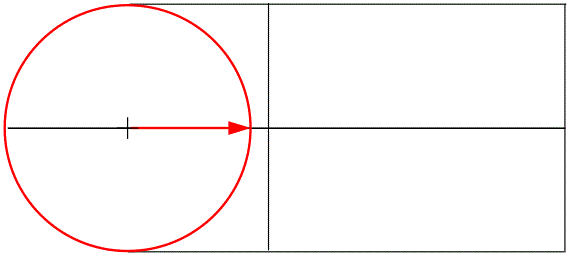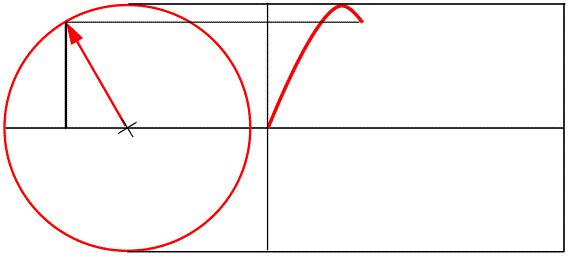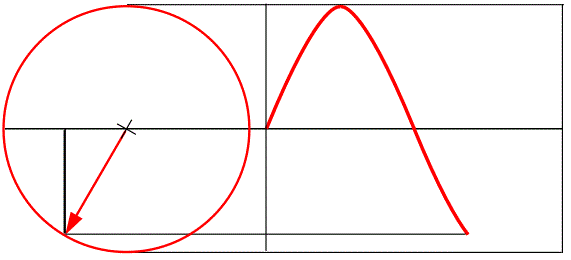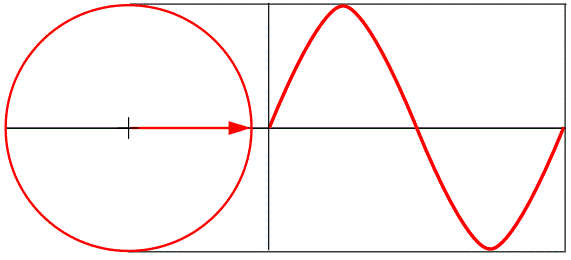
Радиус-вектор рассматривают как вращающийся вокруг точки начала, против часовой стрелки. График синусоиды откладывается на шкале времени вправо. Каждая точка синусоиды получается, как проекция конца радиус вектора в данный момент. А поскольку он крутится, значит, каждое следующее положение вектора, можно определить углом его положения.

Каждая точка синусоиды может быть описана углом положения радиус вектора в данный момент.

Для того, чтобы понятны формулы вспомним, как измеряются углы окружности.

Традиционное измерение в градусах –

360 –вся окружность

270 –три четверти окружности половина

180 – половина окружности

90 - четверть

Анализ синусоиды в градусах неудобен, поэтому используется измерение углов в радианах.

Что такое «ПИ». π – это число, которое показывает сколько раз диаметр окружности укладывается в ее длине – Важнейшая мировая константа, она равна 3,14

Построим в окружности угол так, чтобы радиусы приходили в точки окружности на концах дуги равной тоже радиусу. Таких кусочков дуги укладывается в окружности 6,28 раза, значит, таких углов можно уложить в окружность тоже 6,28.

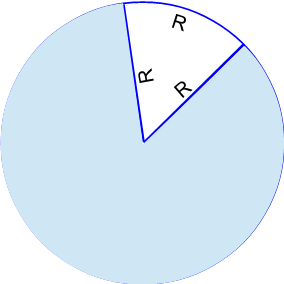
Угол, который опирается на дугу, равную радиусу называется радиан, в окружности 6,28 радиан. А что такое 6,28 – это 2 π, то есть, в окружности 2π радиан.

Тогда просто сравнить и понять

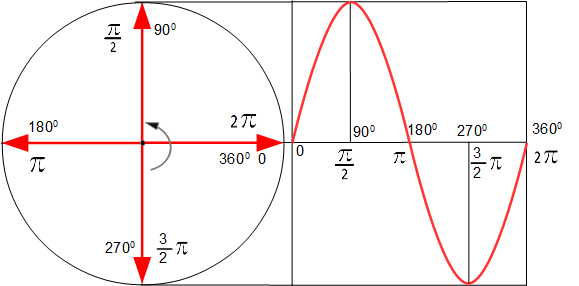
360 –вся окружность 6, 28 радиан - 2 π

270 –три четверти окружности 3 π/2

180 – половина окружности 3,14 радиана - π

90 - четверть окружности π/2

Значит, угол можно измерять в градусах и можно в радианах с коэффициентом π, в нашем случае это гораздо удобнее.

Как протекает переменный синусоидальный процесс во времени? Какой величины будет мгновенное значение переменной через такое-то время? Это зависит от скорости вращения радиус вектора.

Угловая скорость или угловая частота.

Скорость это путь на время. Полный путь вращающегося вектора это 2π -целая окружность, и этот путь надо разделить на время Т, за которое радиус вектор, проходит всю окружность. Время Т называется период вращения. Таким образом угловая частота обозначается ω и равна она 2 π /Т

Теперь у нас есть возможность определить значение переменной величины в любой точке (момент t) , то есть, любое мгновенное значение. Например, мгновенное значение переменного напряжения.

u=UmSin ωt, где t – это мгновение времени от нуля, в которое нас интересует переменная величина.

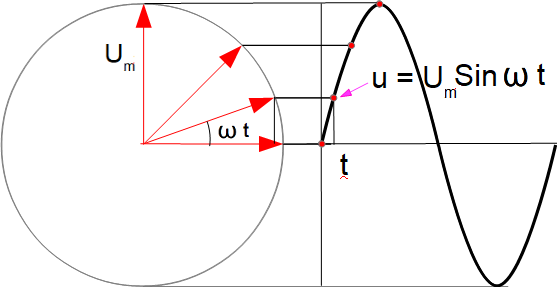
u - мгновенное значение переменного напряжения

Um - максимальное значение переменной величины (радиус –вектор)

Sin ωt – закон изменения переменной величины

Фаза

Фазой называется начальный угол, в котором мы начинаем рассматривать переменный процесс.

В электротехнике начальная фаза нас интересует обычно, когда мы рассматриваем одновременно 2 и больше переменных процесса.

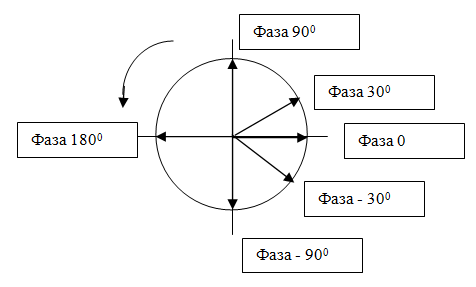
Радиус вектор, вращается против часовой стрелки. Каждое мгновенное положение вектора соответствует определенной фазе.

Сдвиг фаз

Сдвиг фаз позволяет оценить 2 синусоидальных процесса во времени.

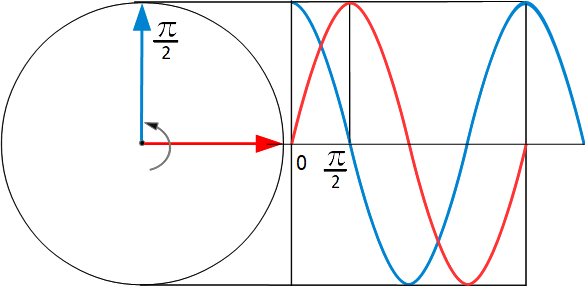
Фаза красной синусоиды - 0, фаза синей синусоиды π/2, когда красная синусоида еще имеет значение 0, синяя уже выросла до максимального значения, синяя синусоида опережает красную по фазе.

Другими словами

Шкала времени синусоиды откладывается вправо от нуля. Если возьмем условно ноль времени за начало отсчета, то видно, что в этот момент мгновенное значение красной синусоиды равно нулю, ее фаза равна 0, в этот же момент синяя синусоида уже имеет максимальное значение, ее фаза π/2 или 90 градусов, Синяя синусоида впереди.

-

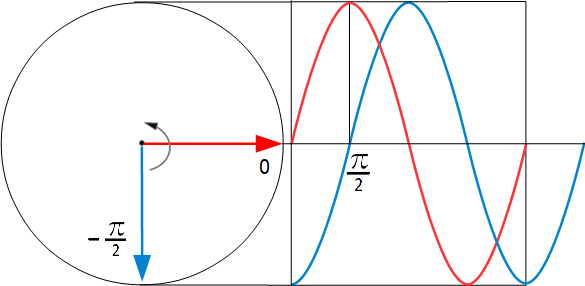
Фаза красной синусоиды - 0, фаза синей синусоиды -π/2, когда красная синусоида уже имеет значение 0, синяя еще в отрицательном максимуме, красная синусоида опережает синюю по фазе.

Начальная фаза - это угол радиус вектора в условный момент, который мы считаем моментом начала процесса. Начальная фаза важна для понимания сдвига фаз между разными переменными процессами.

Начальная фаза обозначается буквой, Ψ и она прибавляется к углу поворота радиус вектора для данного мгновенного значения.

В дальнейшем слово «начальная» мы опускаем и когда говорим «фаза», то подразумеваем, что это начальная фаза.

Синусоида, фаза которой будет больше, опережает ту синусоиду, фаза которой меньше.

Впереди та синусоида, вектора которой повернут на больший угол.

Векторы, смотрящие вверх от горизонтального направления, считаются опережающими, а векторы, смотрящие вниз от горизонтального направления, считаются отстающими или позади.

Пример в движении

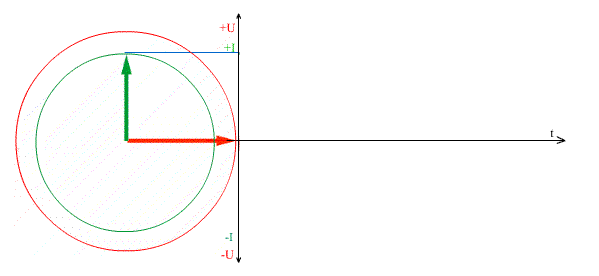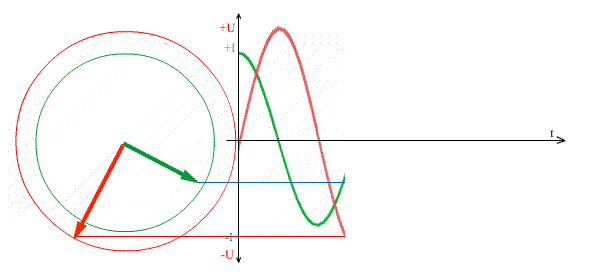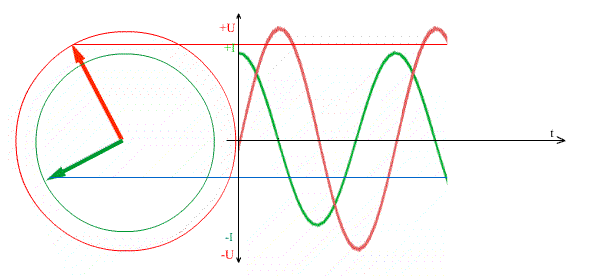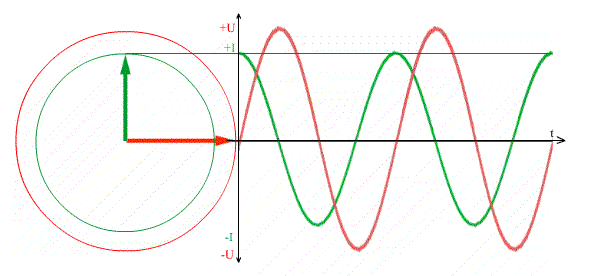
Действующее значение переменной величины

На примере напряжения.

Переменное напряжение все время меняется. Как сказать, какое это напряжение, если оно в каждое следующее мгновение другое. Чтобы объявить значение переменного напряжения, его сравнивают со значением постоянного напряжения, которое дает такой же результат. Например, выделяет на одной и той же лампочке такую же мощность. То есть, если лампочка горит одинаково под переменным напряжением и под постоянным напряжением, значит переменное напряжение по действию равно постоянному.

Такое значение переменного напряжения принято называть действующим.

Для того чтобы получить нужное действующее значение синусоиды, ее амплитуда должна быть в корень из двух раз больше соответствующего значения постоянной величины.

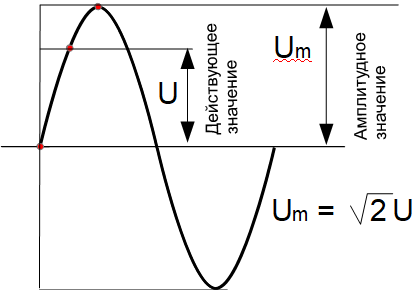
Например, переменное напряжение 220 Вольт – это действующее значение переменного напряжения, Оно дает такой же результат, что и постоянное напряжение 220 Вольт, то есть мы не узнаем, глядя на лампочку, переменное напряжение на ней действует или постоянное.

Оказалось, что чтобы получить действующее напряжение 220 Вольт. Надо создать переменное напряжение, такой величины, чтобы амплитуда напряжение достигала 310 Вольт, то есть, было в корень из двух больше соответствующего действующего.  220 * 1,41= 310

Действующее значение – главная оценка переменной величины и обычно она обозначается символом без индекса, например I, U, E.

Амплитудные значения используют индексы Iа, Uа, Eа , или Im, Um, Em. В практических расчетах оно нас редко интересует.

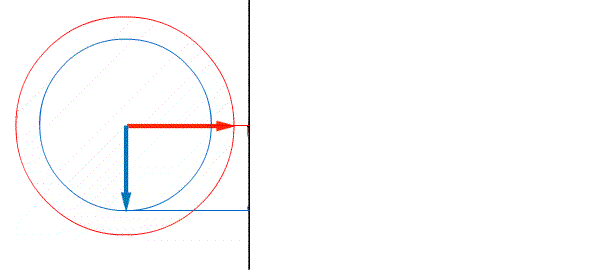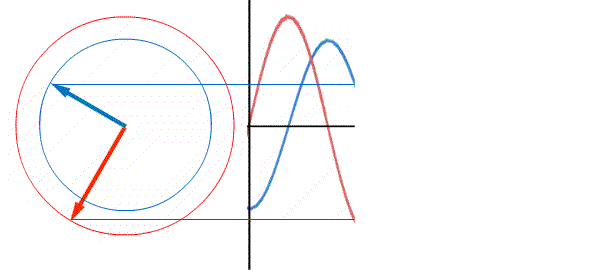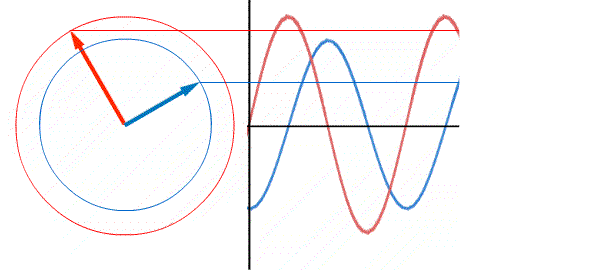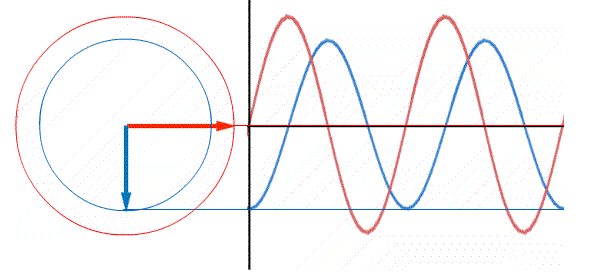
Два синусоидальных процесса сдвинутых по фазе, то есть по времени.

Красная синусоида каждый раз достигает максимума раньше, чем синяя синусоида, значит красная синусоида впереди, то есть она опережает по фазе на 90⁰

Далее рассмотрим простейшие электрические цепи переменного тока

.